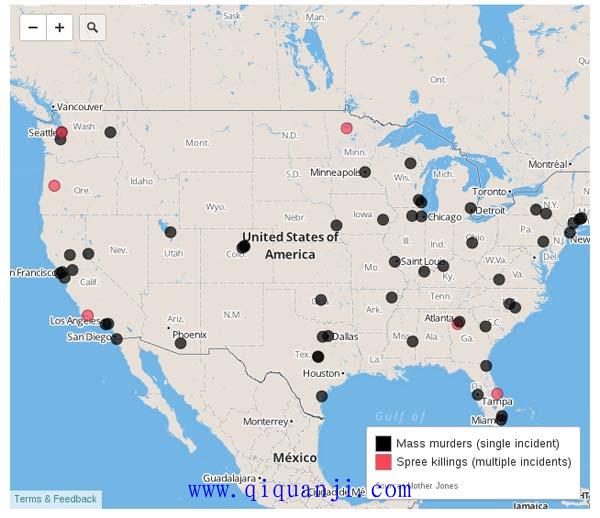
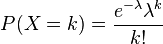泊松分布与美国枪击案

去年12月，美国康涅狄格州发生校园枪击案，造成28人死亡。

资料显示，1982年至2012年，美国共发生62起（大规模）枪击案。其中，2012年发生了7起，是次数最多的一年。

去年有这么多枪击案，这是巧合，还是表明美国治安恶化了？

前几天，我看到一篇很有趣的文章，使用"泊松分布"（Poisson distribution），判断同一年发生7起枪击案是否巧合。

让我们先通过一个例子，了解什么是"泊松分布"。

已知某家小杂货店，平均每周售出2个水果罐头。请问该店水果罐头的最佳库存量是多少？

假定不存在季节因素，可以近似认为，这个问题满足以下三个条件：

（1）顾客购买水果罐头是小概率事件。

（2）购买水果罐头的顾客是独立的，不会互相影响。

（3）顾客购买水果罐头的概率是稳定的。

在统计学上，只要某类事件满足上面三个条件，它就服从"泊松分布"。

泊松分布的公式如下：

各个参数的含义：

　　P：每周销售k个罐头的概率。

　　X：水果罐头的销售变量。

　　k：X的取值（0，1，2，3...）。

　　λ：每周水果罐头的平均销售量，是一个常数，本题为2。

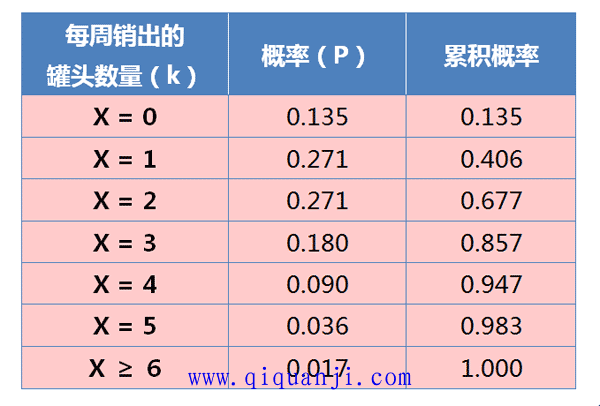
根据公式，计算得到每周销量的分布：

从上表可见，如果存货4个罐头，95%的概率不会缺货（平均每19周发生一次）；如果存货5个罐头，98%的概率不会缺货（平均59周发生一次）。

现在，我们再回过头，来看美国枪击案。

假定它们满足"泊松分布"的三个条件：

　　（1）枪击案是小概率事件。

　　（2）枪击案是独立的，不会互相影响。

　　（3）枪击案的发生概率是稳定的。

显然，第三个条件是关键。如果成立，就说明美国的治安没有恶化；如果不成立，就说明枪击案的发生概率不稳定，正在提高，美国治安恶化。

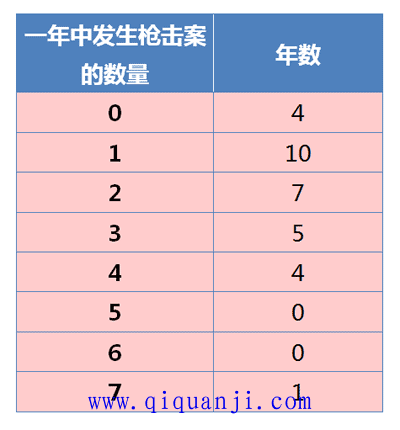
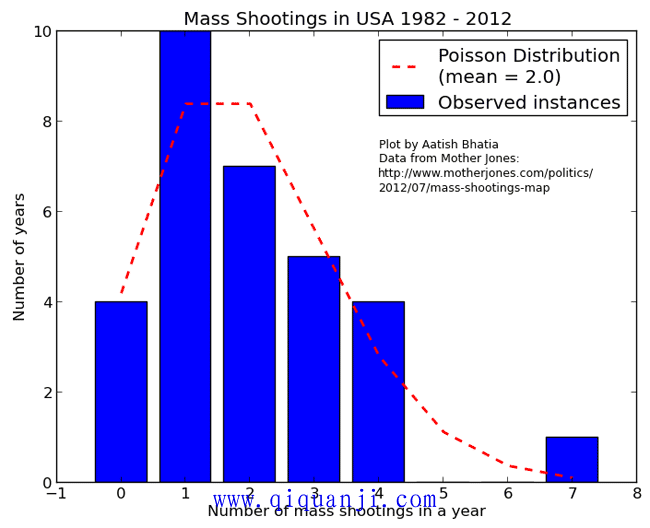
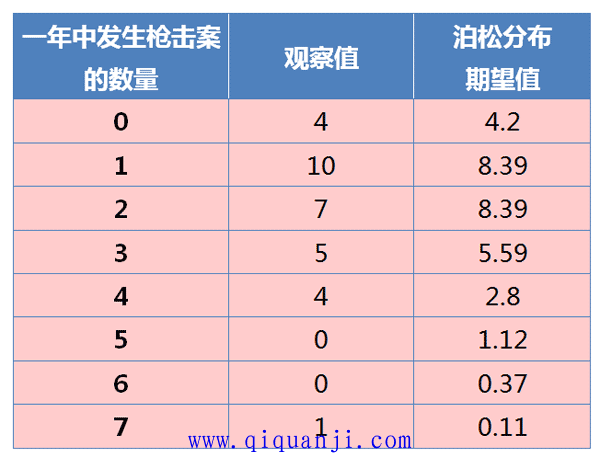
根据资料，1982--2012年枪击案的分布情况如下：

计算得到，平均每年发生2起枪击案，所以 λ = 2 。

上图中，蓝色的条形柱是实际的观察值，红色的虚线是理论的预期值。可以看到，观察值与期望值还是相当接近的。

我们用"卡方检验"（chi-square test），检验观察值与期望值之间是否存在显著差异。

　　卡方统计量 = Σ [ ( 观察值 - 期望值 ) ^ 2 / 期望值 ]

计算得到，卡方统计量等于9.82。查表后得到，置信水平0.90、自由度7的卡方分布临界值为12.017。因此，卡方统计量小于临界值，这表明枪击案的观察值与期望值之间没有显著差异。所以，可以接受"发生枪击案的概率是稳定的"假设，也就是说，从统计学上无法得到美国治安正在恶化的结论。

但是，也必须看到，卡方统计量9.82离临界值很接近，p-value只有0.18。也就是说，对于"美国治安没有恶化"的结论，我们只有82%的把握，还有18%的可能是我们错了，美国治安实际上正在恶化。因此，这就需要看今后两年中，是否还有大量枪击案发生。如果确实发生了，泊松分布就不成立了。

[参考阅读]

　　* 泊松分布，by 曹亮吉

　　* 卡方分布（PDF文件）

原文链接：https://www.qiquanji.com/post/6913.html

本站声明:网站内容来源于网络,如有侵权,请联系我们,我们将及时处理。