匈牙利算法

匈牙利算法：它由匈牙利数学家Edmonds于1965年提出，因而得名。此算法的核心就是寻找增广路径，通过增广路径来求二分图最大匹配的一种算法。

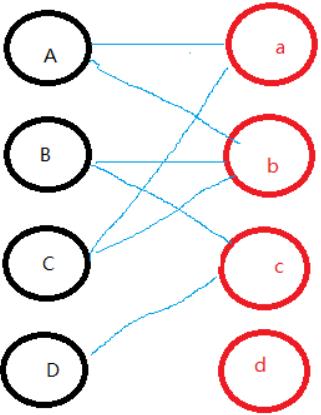
通过这个图片来讲述一下。黑色代表A\B\C\D四只小狗，红色代表四种口味的骨头，每一条线表示的是小狗喜欢吃这个口味的骨头。

我们按照顺序给小狗们分配骨头，先给A分配，很明显a无人占用并且小A狗很喜欢，分配，博主最喜欢成人之美。(◡‿◡)

现在给小B狗分配，小B喜欢b，前提b无人占用并且小B心仪很久，又成全一只小狗，哇哈哈~~

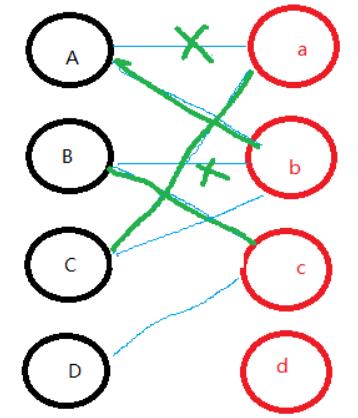
轮到小C狗了，小C等了好久了，但是小C喜欢的骨头全都被占了，好可怜有木有，但是没关系，我们想办法来帮助他。如下图。

通过这张图，我们可以很清晰的知道，我们把A的先拿掉，但是还是要给找一个，不然岂不是太偏心，给A找到b，但是b被占了，同理，也先拿掉，这样A满足了,在给B继续找， 这样我们就找到c，ok大家都可以找到后备胎了，那么小C可以吃a！！！同理对d一样，但是发现如果满足d，其他的都会被破坏，综上，得到最大的匹配值为3。

匈牙利算法的流程就是上述的方案。

以下是一些技巧总结:

二分图的最小顶点覆盖：在二分图中求最少的边，让每条边至少和其中的一个点关联

最小顶点覆盖=最大匹配数

DAG图（无回路有向图(Directed Acyclic Graph)）的最小路径覆盖：用尽量少的不想交的简单路径覆盖图中的所有顶点

最小路径覆盖=顶点数-最大匹配数

无向图的最小路径覆盖：

无向二分图的最下路径覆盖=顶点数-最大二分匹配/2（因为无向图就是双向的一条边等于两次入图正向和反向，最后得到的匹配数多了一倍所以要除以2才是原本的匹配数）

点可以重复走的最小路径覆盖：

【题意】：派机器人去火星寻宝，给出一个无环的有向图，机器人可以降落在任何一个点上，再沿着路去其他点探索，我们的任务是计算至少派多少机器人就可以访问到所有的点。有的点可以重复去。

【思路】：我们仍可将问题转换为最小路径覆盖。如果一个人需要经过另一个人走过的点时候，让他直接从该点上空飞过去，越过该点，直接走下一个点。如果我们赋予每个人这种能力，那么求得的无重复点的最小路径覆盖结果，就是题目要求的结果，因为需要重复的地方只要飞过去，就可以不重复了。赋予这个能力的方法就是吧所有点能间接到达的点全都改为直接到达。

二分图的最大独立集：在二分图中任意两点都不相邻的顶点的最大集合

最大独立集=结点数-最大匹配数

二部图的多重匹配：一般的二部图只能匹配一个点，在多重匹配中，一个点可以匹配多给点

本文最后编辑：2019-07-18  09:07:18 

原文链接：https://www.qiquanji.com/post/8418.html

本站声明:网站内容来源于网络,如有侵权,请联系我们,我们将及时处理。